Spin Hall effects are a collection of relativistic spin-orbit coupling phenomena in which electrical currents can generate transverse spin currents and vice versa. one can draw an analogy using the Magnus force, which is well known in sports with rotating balls (Link). Despite being observed only a decade ago, these effects are already ubiquitous within spintronics, as standard spin-current generators and detectors. You can find a complete overview of this field in our recent comprehensive Reviews of Modern Physics article, which was featured on the journal cover (Link)
We are currently working on spin Hall effect in graphene devices.
We have pioneered novel detection techniques [Nature 442, 176 (2006)] that led to the first demonstration of direct detection of spin currents, and the first electrical measurements of the (reciprocal) spin Hall effect (SHE). The SHE is the generation in a non-magnetic sample of a spin current transverse to an applied charge current that results in spin accumulation near the lateral edges with opposite polarization. This effect was first predicted over three decades ago, and more recently independently rediscovered, by invoking the phenomenology of the anomalous Hall effect in ferromagnets. The SHE was associated to asymmetric Mott-skew and side-jump scattering from impurities in a spin-orbit coupled system. It was pointed out that after scattering off an impurity there should be a spin dependent probability difference in the electron trajectories with opposite spins, which would induce the spin accumulation. More recently, the intrinsic spin-orbit coupling mechanism, that is inherent to the band structure and is finite away from impurities, has also been considered and the existence of an intrinsic SHE has been proposed, where impurities play a minor role.
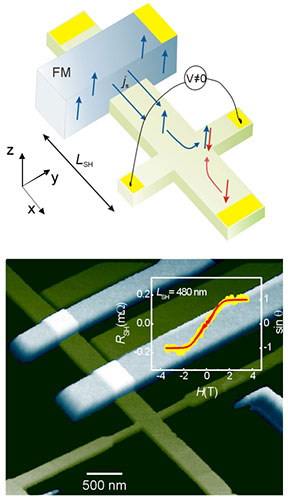
Measurement of the Spin Hall Effect. Sample Scheme (top) and AFM micrograph of a sample (bottom)
We are currently interested in the quantum analogous of the spin Hall effect, that is, the quantum spin Hall effect. The quantum spin Hall phase is a topological phase in the sense that certain fundamental properties are insensitive to small changes in material parameters. For these fundamental properties to change there should be a phase transition. The phase can be generalized to three dimensions and is usually known as a topological insulator. It is characterized by an insulating bulk and gapless states localized in the system boundaries when placed in vacuum or in contact with any other common insulator. These metallic boundaries originate from topological invariants and cannot change as long as the bulk remains insulating or time reversal symmetry at the surface is not broken. In a simple two dimensional (2D) picture, topological insulators can be understood as two copies of the integer quantum Hall effect. As opposed to the quantum Hall effect, there are both forward and backward movers. In the three dimensional case, the surface state (or interface with an ordinary insulator) can be described, in the simplest case, by two-dimensional massless Dirac fermions (as in graphene) with a dispersion forming a Dirac cone with the crossing point located at the time reversal invariant momentum k = 0. The degeneracy at k = 0 and the surface metallic states are protected by time inversion symmetry and electrons traveling on such a surface state are weakly sensitive to impurity scattering and their spins have opposite orientation at momenta k and -k. The spin arrangement contributes a Berry phase of pi to the wavefunction protecting the surface states against backscattering by nonmagnetic impurities. More information can be found in the book Spin Current. We are organizing a workshop on this topic and working on novel ways to characterize the surface states.
